이진 탐색 트리 (Binary Search Tree)
06 Jul 2020 | Data Structure
본 게시물은 문일철 교수님의 데이터 구조 및 분석을 참조하여 작성하였습니다.
이진 탐색 트리 (Binary Search Tree)
이진 탐색 트리(Binary Search Tree, BST) 는 차수(Degree)가 2인 트리입니다. 연결된 리스트(Linked List)가 해결해주지 못하는 탐색(Search)을 최적화하기 위해 고안된 자료구조입니다. 이런 특성 때문에 이름에도 탐색(Search)이 붙었습니다. 이진 탐색 트리가 데이터를 빠르게 탐색할 수 있는 비결은 무엇일까요? 해답은 이진 탐색 트리가 데이터를 보관하는 방법에 대한 특별한 규칙(Rule)에 있습니다. 아래는 한 이진 탐색 트리의 예시입니다.

이미지 출처 : 위키피디아 - 이진 탐색 트리
위 트리에는 어떤 규칙이 있는 것일까요? 루트와 그 자식 노드에 해당하는 두 노드를 봅시다. 루트의 값은 8이며 왼쪽 자식 노드의 값은 3, 오른쪽 자식 노드의 값은 10입니다. 루트를 기준으로 더 작은 값은 왼쪽 자식 노드로, 더 큰 값은 오른쪽 자식 노드로 배치된 것을 볼 수 있습니다. 다음에는 아래로 내려가 값이 3인 노드와 그 자식 노드를 봅시다. 이 세 노드도 마찬가지로 3보다 작은 값인 1은 왼쪽 자식 노드로, 6은 오른쪽 자식 노드로 배치된 것을 볼 수 있습니다.
이진 탐색 트리의 모든 값은 이 규칙을 따라 배치됩니다. 부모 노드보다 값이 큰 노드는 오른쪽에, 값이 작은 노드는 왼쪽에 배치됩니다. 이런 규칙이 있기 때문에 더욱 빠르게 찾을 수 있습니다. 연결된 리스트에서의 탐색 과정과 비교해 보겠습니다. $8, 3, 10, 1, 6, 14, 4, 7, 13$ 이 차례대로 저장된 연결된 리스트와 이진 탐색 트리가 있다고 해봅시다. 연결된 리스트에서 $13$ 을 찾기 위해서는 모든 요소와 비교를 해야 하므로 총 9번의 Operation을 거쳐야 합니다. 하지만 이진 탐색 트리에서는 $8, 10, 14, 13$ 만 비교하면 되니 4번의 Operation 만으로 원하는 탐색을 할 수 있습니다. 이진 탐색 트리의 탐색에 대해서는 아래에서 더 자세히 살펴보겠습니다.
Structure
연결된 리스트의 노드 하나에는 총 2개의 레퍼런스가 있었습니다. 하나는 값을 가리키는 레퍼런스이고 나머지 하나는 다음 노드를 가리키는 레퍼런스로, 넥스트(Next)라고 불렀습니다. 이진 탐색 트리는 가리켜야 하는 노드가 2개이기 때문에 총 3개의 레퍼런스를 가지고 있습니다. 그 중 왼쪽 자식 노드를 가리키는 레퍼런스를 LHS(Left Hand Side)라고 하고, 오른쪽 자식 노드를 가리키는 레퍼런스는 RHS(Right Hand Side)라고 합니다.
연결된 리스트가 헤드를 통해서만 다른 노드에 접근할 수 있었던 것처럼 트리 역시 첫 번째에 해당하는 루트를 통해서만 다른 노드에 접근할 수 있습니다. 아래는 이진 탐색 트리의 노드를 파이썬 코드로 구현한 것입니다.
class TreeNode:
nodeLHS = None
nodeRHS = None
nodeParent = None
value = None
def __init__(self, value, nodeParent):
self.value = value
self.nodeParent = nodeParent
"""각 레퍼런스 설정하기"""
def getLHS(self):
return self.nodeLHS
def getRHS(self):
return self.nodeRHS
def getParent(self):
return self.nodeParent
def getValue(self):
return self.value
def setLHS(self):
self.nodeLHS = nodeLHS
def setRHS(self):
self.nodeRHS = nodeRHS
def setParent(self):
self.nodeParent = Parent
def setValue(self):
self.value = value
아래는 이진 탐색 트리의 루트와 이진 탐색 트리에서 가능한 여러 Operation을 파이썬 코드로 적어놓은 것입니다.
from bst import TreeNode
class BinarySearchTree:
root = None
def __init__(self):
pass
def insert(self, value, node=None):
"..."
def search(self, value, node=None):
"..."
def delete(self, value, node=None):
"..."
def findMax(self, node=None):
"..."
def findMin(self, node=None):
"..."
def traverseLevelOrder(self):
"..."
def traverseInOrder(self, node=None):
"..."
def traversePreOrder(self, node=None):
"..."
def traversePostOrder(self, node=None):
"..."
이진 탐색 트리에서의 탐색
이진 탐색 트리 속에 우리가 원하는 값이 있는지 없는지 탐색(Search)하는 과정을 알아봅시다. 이진 탐색 트리에서 데이터를 저장할 때 세웠던 규칙이 빛을 발할 때가 되었습니다. 탐색하려는 값이 우리가 보고 있는 노드의 값보다 클 경우에는 RHS를 따라 이동하고, 작을 경우에는 LHS를 따라 이동합니다. 이전처럼 우리가 원하는 값을 발견할 경우에는 True를 반환하고 그렇지 않은 경우에는 다시 같은 과정을 재귀적으로(Recursive) 수행합니다. 재귀적으로 아래쪽으로 내려가다가 자식 노드가 없을 경우, 즉 리프 노드의 값이 우리가 원하는 값이 아닐 경우에는 False를 반환하고 함수를 끝마칩니다.
위에서 사용한 예시를 다시 가져와 보겠습니다.

이미지 출처 : 위키피디아 - 이진 탐색 트리
위와 같은 이진 탐색 트리에서 $13$ 을 찾기 위해서는 어떻게 해야할까요? 가장 먼저 할 수 있는 것은 루트 노드로 접근하여 값을 비교하는 것입니다. $13$ 은 $8$ 보다 크므로 RHS를 따라 이동합니다. 다음 노드의 값은 $10$ 입니다. $13$ 은 $10$ 보다도 크기 때문에 또 RHS를 따라 이동합니다. 다음 노드의 값은 $14$ 입니다. $13$ 은 $14$ 보다 작기 때문에 LHS를 따라 이동합니다. 그 다음 노드의 값이 우리가 찾던 $13$ 이므로 True를 반환하고 함수를 마칩니다.
트리에 없는 값을 탐색하는 과정도 보겠습니다. $5$ 는 어떻게 탐색할 수 있을까요? 나머지 규칙은 위와 같습니다. 루트로 접근하여 $5$ 가 $8$ 보다 작으므로 LHS를 따라 이동, $3$ 보다는 크므로 RHS를 따라 이동, $6$ 보다는 작으므로 LHS를 따라 이동합니다. 다음 노드의 값은 $4$ 입니다. $5$ 가 $4$ 보다 크기 때문에 RHS를 따라 이동해야 하는데 더 이상 이동할 노드가 없습니다. 그러므로 False를 반환하고 함수를 마치게 됩니다.
아래의 코드는 이진 탐색 트리에서의 탐색을 파이썬 코드로 구현한 것입니다.
def search(self, value, node=None):
"""
같은 값을 발견하면 True를 반환하도록 합니다.
"""
if node is None:
node = self.root
if value == node.getValue():
return True
"""
그렇지 않은 경우 크기비교를 하며 RHS, LHS로 나아가게 되고
일치하는 값을 찾지 못하고 빈 노드를 만나면 False를 반환합니다.
"""
if value > node.getValue():
if node.getRHS() is None:
return False
else:
return self.search(value, node.getRHS())
if value < node.getValue():
if node.getLHS() is None:
return False
else:
return self.search(value, node.getLHS())
이진 탐색 트리에서의 삽입
이진 탐색 트리에서의 삽입(Insert)하는 과정에 대해 알아봅시다. 삽입은 탐색과 매우 유사합니다. 삽입을 규칙에 맞게 하기 때문에 탐색이 쉬운 것이니까요.
삽입 역시 삽입 하려는 값이 해당 노드보다 작으면 LHS를 따라 이동하고, 크면 RHS를 따라 이동하는 과정을 재귀적으로 반복합니다. 탐색에서 원하는 값이 발견되면 True를 반환하였지만, 삽입은 원하는 값이 있으면 아무것도 반환하지 않고 그대로 함수를 마칩니다. 그리고 탐색에서는 더 이상 내려갈 자식 노드가 없으면 False를 반환했지만, 삽입에서는 그 자리에 우리가 원하는 값이 담긴 노드를 배치하고 함수를 마치게 됩니다. 삽입도 같은 예시를 통해 알아봅시다.

이미지 출처 : 위키피디아 - 이진 탐색 트리
탐색 과정에서 트리에 없었던 $5$ 를 삽입해 보겠습니다. 탐색과 같은 과정을 거쳐 $8, 3, 6, 4$ 를 따라 이동합니다. 탐색은 $4$ 이하에 RHS를 따라 이동할 노드가 없었기 때문에 False를 반환했지만 삽입은 그 자리에 $5$ 를 삽입하고 함수를 마치게 됩니다.
아래의 코드는 이진 탐색 트리에서의 삽입을 파이썬 코드로 구현한 것입니다.
def insert(self, value, node=None):
"""
재귀 탈출 조건문 설정하기
노드가 채워져 있지 않을 경우에는 값을 할당하도록 되어있습니다.
"""
if node is None:
node = self.root
if self.root is None:
self.root = TreeNode(value, None)
return
"""
값이 같을 경우 그대로 반환
값이 큰 경우 RHS를 따라 이동하여 재귀를 통해 같은 함수를 실행
값이 작은 경우 LHS를 따라 이동하여 재귀를 통해 같은 함수를 실행
둘 모두 값이 존재하지 않을 경우에는 해당 값을 할당하도록 합니다.
"""
if value == node.getValue():
return
if value > node.getValue():
if node.getRHS() is None:
node.setRHS(TreeNode(value, node))
else:
self.insert(value, node.getRHS())
if value < node.getValue():
if node.getLHS() is None:
node.setLHS(TreeNode(value, node))
else:
self.insert(value, node.getLHS())
return
이진 탐색 트리에서의 삭제
다음은 삭제를 알아볼 차례입니다. 이진 탐색 트리에서의 삭제는 이전의 자료 구조보다 훨씬 더 까다롭습니다. 이진 탐색 트리에서 노드를 삭제하는 경우의 수는 3개이므로 각각을 나누어 생각해야 합니다.
첫 번째는 자식 노드를 갖지 않는, 즉 리프 노드의 값을 삭제하는 경우입니다. 가장 간단한 케이스이기도 합니다. 이 때는 해당 노드의 부모 노드가 가리키는 레퍼런스를 제거함으로써 값을 삭제할 수 있습니다. 아래 그림을 봅시다.
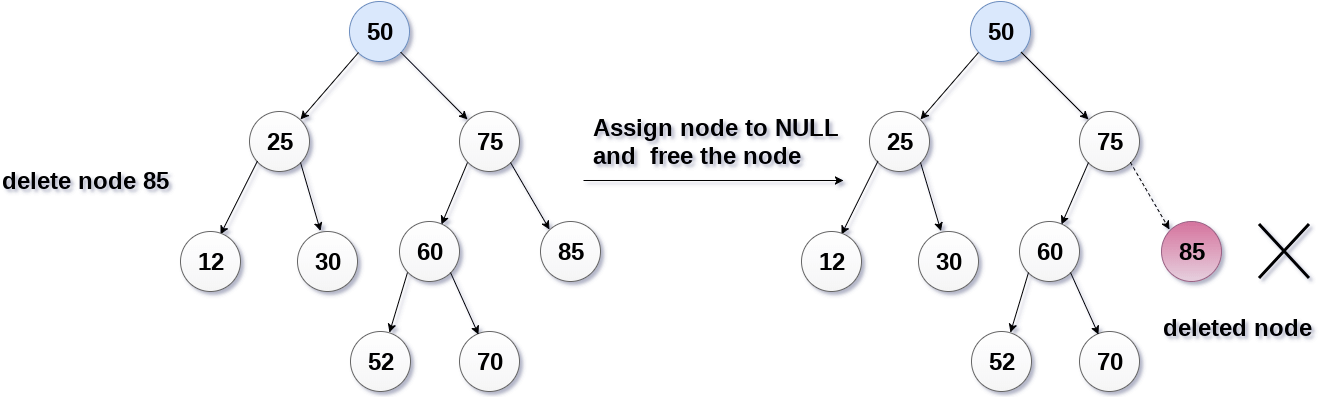
이미지 출처 : javatpoint.com
위 그림은 85를 삭제하는 과정을 이미지로 나타낸 것입니다. 이 노드를 가리키고 있는 부모 노드의 레퍼런스를 제거하면 아무 노드의 가리킴도 받지 않는 85가 있는 노드는 가비지 컬렉터(Garbage collector)에 의해서 삭제됩니다.
두 번째는 하나의 자식 노드를 갖는 노드의 값을 삭제하는 경우입니다. 이 케이스는 연결된 리스트에서 요소를 삭제하는 경우와도 유사합니다. 방법은 삭제하려는 값이 담긴 노드를 가리키는 레퍼런스를 그 자식 노드를 가리키도록 하게 됩니다. 아래 그림을 보겠습니다.
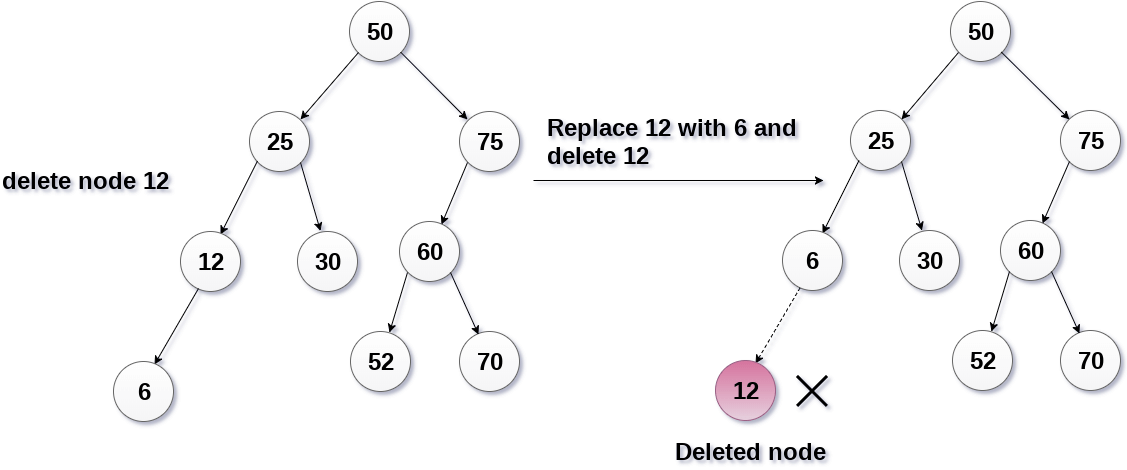
이미지 출처 : javatpoint.com
위 그림은 12를 삭제하는 과정을 이미지로 나타낸 것입니다. 이 노드를 가리키고 있는 레퍼런스를 12가 있는 자식 노드인 6을 가리키도록 합니다. 이전 케이스와 같이 아무 레퍼런스의 가리킴도 받지 못하게 된 12는 가비지 컬렉터에 의해서 사라지게 됩니다.
마지막은 삭제하려는 값이 있는 노드가 두 개의 자식 노드를 갖는 경우입니다. 가장 까다로운 경우입니다. 기본적인 아이디어는 기존에 트리에 존재하는 다른 값으로 대체하여 넣어준 뒤에 중복되는 값을 삭제하는 것입니다. 아래 그림을 보겠습니다.

이미지 출처 : 데이터 구조 및 분석 수업자료
이번 케이스는 2가지 경우의 수가 있습니다. 위 그림은 맨 아래에 있는 이진 탐색 트리에서 $3$ 을 제거할 때의 2가지 경우의 수를 나타낸 것입니다.
왼쪽 경로는 $3$ 대신 $4$ 를 복사해 넣은 후 $4$ 에 해당하는 리프 노드를 삭제하는 과정으로 이루어져 있습니다. 리프 노드는 첫 번째로 알아보았던 그리고 오른쪽 경로는 $3$ 대신 $2$ 를 복사해 넣은 후 원래 $2$ 가 있던 노드를 삭제하는 과정으로 이루어져 있지요. 이렇게 새롭게 생성된 이진 탐색 트리는 기존의 규칙을 깨뜨리지 않습니다. 왼쪽 경로에서 $4$ , 오른쪽 경로에서 $2$ 라는 값은 어떻게 선택되는 것일까요?
일단 아무 값이나 선택하는 것은 안됩니다. 예를 들어, $3$ 이 있던 자리에 $0$ 을 넣고 원래 $0$ 이 있는 노드를 삭제하게 되면 트리의 규칙이 깨져버리기 때문입니다. 선택하는 논리는 비교적 간단합니다. $3$ 보다 왼쪽에 있는 하위 트리(Sub tree)에서는 가장 큰 값을, 오른쪽에 있는 하위 트리에서는 가장 작은 값을 선택하면 됩니다.
왼쪽에 있는 하위 트리에서 가장 큰 값이라도 오른쪽 하위 트리의 모든 값보다는 작으므로 이 값을 삭제하려는 노드에 중복시켜 넣어준 후 원래 노드를 삭제시키면 트리의 규칙을 어기지 않습니다. 오른쪽에 있는 하위 트리에서 가장 작은 값 역시 왼쪽 하위 트리에 있는 모든 값보다는 크기 때문에 삭제하려는 노드에 중복해준 후 원래 값이 있는 노드를 삭제시켜도 트리의 규칙을 어기지 않음을 알 수 있습니다.
트리에서 이런 값을 찾는 방법 역시 간단합니다. 먼저 왼쪽 하위 트리의 최댓값을 찾는 경우 (그림에서 오른쪽 경로) 부터 생각해봅시다. 이 경우는 삭제하려는 값이 있는 노드의 LHS를 따라 한 번 내려간 뒤, 이후부터는 항상 RHS만을 따라갑니다. 만약 더 이상 RHS가 없는 노드가 있다면 그 노드의 값이 중복해줄 값으로 선택됩니다. 위의 예시에서도 $3$ 이 있는 노드의 LHS를 따라 한 번 내려가면 $2$ 가 있는 노드가 됩니다. 다음부터는 RHS 만을 따라 내려가야 하지만 해당 노드에서 RHS가 없으므로 해당 노드의 값인 $2$ 가 삭제할 값을 대체하는 값이 됩니다. 다음으로 오른쪽 하위 트리의 최솟값을 찾는 경우 (그림에서 왼쪽 경로) 를 생각해봅시다. 위 그림에서 왼쪽 방향에 있는 3을 4로 대체한 것은 첫 번째 방법을 따른 것이고, 오른쪽 방향에 있는 3을 2로 대체한 것은 두 번째 방향을 따른 것이다. 이 때는 반대로 삭제하려는 값이 있는 노드의 RHS를 따라 한 번 내려간 뒤, 이후부터는 항상 LHS만을 따라갑니다. 그리고 더 이상 LHS가 없는 노드가 있다면 그 노드의 값이 중복해줄 값으로 선택됩니다. 위의 예시에서도 $3$ 이 있는 노드의 RHS를 따라 한 번 내려가면 $5$ 가 있는 노드가 됩니다. 다음부터는 LHS 만을 따라 내려가야 하므로 한 번 더 이동한 노드의 값은 $4$ 입니다. 다음에 또 LHS를 따라 이동해야 하지만 해당 노드에서 LHS가 없으므로 해당 노드의 값인 $4$ 가 삭제할 값을 대체하는 값이 됩니다.
이렇게 복제된 값을 담고 있는 노드는 LHS나 RHS 중 하나의 레퍼런스가 없는 노드이므로 위에서 나왔던 리프 노드를 삭제하는 방법이나, 자식 노드가 하나인 노드를 삭제하는 방법을 사용하여 처리가 가능합니다. 아래는 모든 삭제 과정을 파이썬 코드로 구현한 것입니다.
def delete(self, value, node=None):
if node is None:
node = self.root
"""
삭제하려는 값을 찾아가는 과정
"""
if node.getValue() < value:
return self.delete(value, node.getRHS())
if node.getValue() > value:
return self.delete(value, node.getLHS())
"""
삭제하려는 값이 있는 노드를 만났을 때
"""
if node.getValue() == value:
"""
2개의 자식을 갖는 노드의 값 삭제하기
여기서는 2가지 방법 중
RHS로 이동 후 RHS에서 가장 왼쪽 값(최솟값)을
찾아 대체하는 방법을 사용하였습니다.
"""
if node.getLHS() is not None and node.getRHS() is not None:
nodeMin = self.findMin(node.getRHS())
node.setValue(nodeMin.getValue())
self.delete(nodeMin.getValue(), nodeRHS())
return
parent = node.getParent()
"""
자식 노드를 1개 갖는 노드의 값을 삭제하는 코드입니다.
"""
if node.getLHS() is not None:
if node == self.root:
self.root = node.getLHS()
elif parent.getLHS() == node:
parent.getLHS(node.getLHS())
node.getLHS().setParent(parent)
else:
parent.setRHS(node.getLHS())
node.getLHS().setParent(parent)
return
if node.getRHS() is not None:
if node == self.root:
self.root = node.getRHS()
elif parent.getLHS() == node:
parent.getLHS(node.getRHS())
node.getRHS().setParent(parent)
else:
parent.setRHS(node.getRHS())
node.getRHS().setParent(parent)
return
"""
자식을 갖지 않는 노드의 값을 삭제하는 경우입니다.
"""
if node == self.root:
self.root = None
elif parent.getLHS() == node:
parent.setLHS(None)
else:
parent.setRHS(None)
return
위 코드에 있는 findMax 와 findMin 함수 역시 따로 정의를 해주어야 합니다. 아래와 같이 각 함수를 정의할 수 있습니다.
def findMax(self, node=None):
if node is None:
node = self.root
if node.getRHS() is None:
return node
return self.findMax(node.getRHS())
def findMin(self, node=None):
if node is None:
node = self.root
if node.getLHS() is None:
return node
return self.findMin(node.getLHS())
Traversing
Traverse는 ‘가로지르다’라는 뜻을 가진 단어입니다. 연결된 리스트나 배열에서 존재하지 않았던 Traversing 이란 말 그대로 모든 노드를 가로지르며 값을 훑는 것입니다. 이전에 배웠던 자료구조는 중간에 갈라지는 길이 없으므로 탐색(Search)하면서 모든 노드를 다 거칠 수 있었습니다. 하지만 트리에서는 길이 나누어지므로 값을 찾는 탐색만으로 모든 노드를 거쳐갈 수 없게 되지요.
Traversing의 방법은 크게 깊이 우선 탐색법(Depth first search, DFS) 과 너비 우선 탐색법(Breadth first search, BFS) 두 가지로 나뉩니다. 먼저 깊이 우선 탐색법에 대해 알아봅시다. 깊이 우선 탐색법은 순서에 따라 3가지 방법이 있습니다. 첫 번째가 현재 노드의 값을 탐색한 후 LHS, RHS 순서로 탐색하는 Pre-order Traverse 입니다. 두 번째는 LHS를 먼저 탐색하고 현재 노드의 값을 탐색한 후 RHS값을 탐색하는 In-order Traverse 입니다. 마지막 방법으로는 LHS와 RHS를 모두 탐색한 후 맨 마지막에 현재 노드의 값을 탐색하는 Post-order Traverse가 있습니다. 아래의 트리를 보며 설명을 이어나가겠습니다. 아래의 노드를 각 방법으로 Traversing 해보겠습니다.

이미지 출처 : towardsdatascience.com
먼저 Pre-order 방식입니다. 앞서 말했던 것처럼 이 방식은 현재 노드 - LHS를 따라 내려간 노드 - RHS를 따라 내려간 노드 순으로 탐색합니다. 아래 그림과 같은 방법으로 탐색이 이루어집니다. 접근하는 노드의 값을 무조건 얻기 때문에 루트 노드 부터 탐색하는 것을 볼 수 있습니다.

이미지 출처 : towardsdatascience.com
다음은 In-order 방식입니다. 이 방식은 LHS를 따라 내려간 노드 - 현재 노드 - RHS를 따라 내려간 노드 순으로 탐색합니다. 아래 그림과 같은 방법으로 탐색이 이루어집니다. 현재 노드의 값을 얻지 않고 일단 LHS가 없을 때까지 내려가기 때문에 가장 왼쪽 아래에서부터 탐색이 시작되는 것을 볼 수 있습니다.
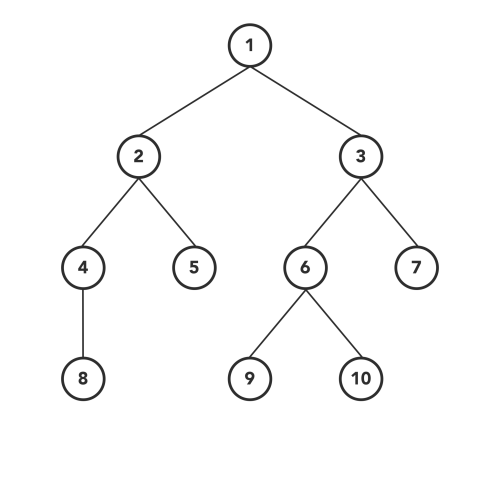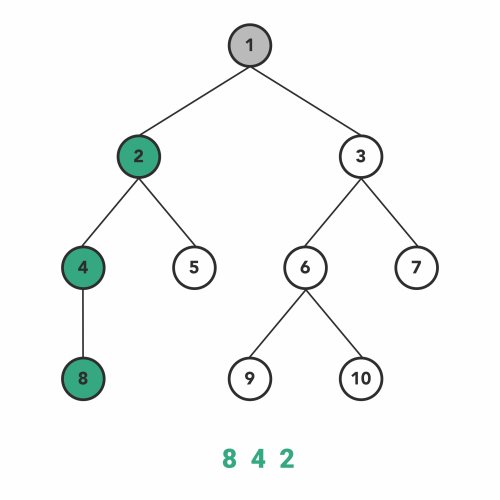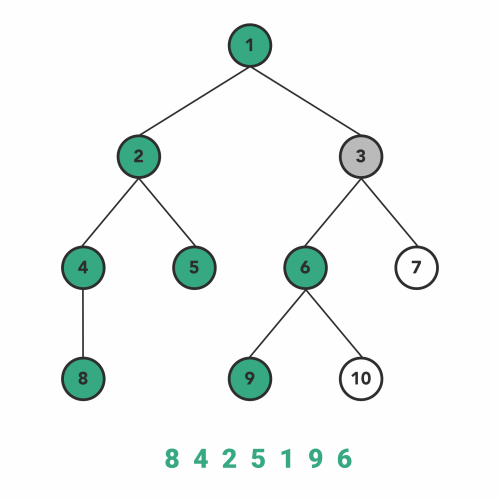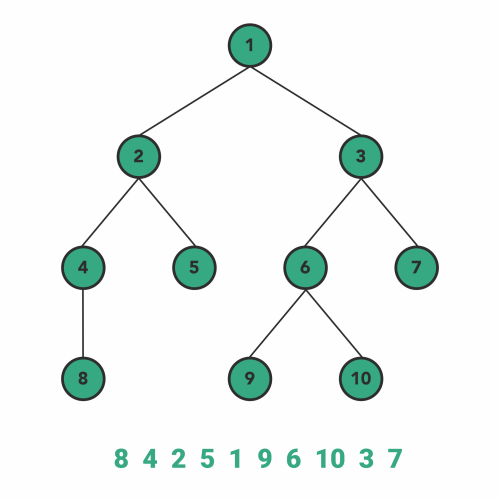
이미지 출처 : towardsdatascience.com
다음은 Post-order 방식입니다. 이 방식은 LHS를 따라 내려간 노드 - RHS를 따라 내려간 노드 - 현재 노드 순으로 탐색합니다. 아래 그림과 같은 방법으로 탐색이 이루어집니다. 현재 노드의 값을 얻지 않고 일단 LHS와 RHS가 모두 없을 때까지 내려가기 때문에 가장 왼쪽 아래에서부터 아래쪽을 다 훑고 난 후에 위로 올라오는 방향으로 탐색이 되는 것을 볼 수 있습니다.

이미지 출처 : towardsdatascience.com
각각의 깊이 우선 탐색 과정을 파이썬 코드로 구현하면 다음과 같습니다.
"""
일단 현재 노드의 값을 추가한 뒤
LHS, RHS 순으로 탐색합니다.
"""
def traversePreOrder(self, node=None):
if node is None:
node = self.root
ret = []
ret.append(node.getValue())
if node.getLHS() is not None:
ret = ret + self.traversePreOrder(node.getLHS())
if node.getRHS() is not None:
ret = ret + self.traversePreOrder(node.getRHS())
return ret
"""
일단 현재 LHS 부분부터 최대한 탐색한 뒤
현재 노드의 값을 추가하고 그 다음 RHS 부분을 탐색합니다.
"""
def traverseInOrder(self, node=None):
if node is None:
node = self.root
ret = []
if node.getLHS() is not None:
ret = ret + self.traversePreOrder(node.getLHS())
ret.append(node.getValue())
if node.getRHS() is not None:
ret = ret + self.traversePreOrder(node.getRHS())
return ret
"""
일단 현재 LHS 부분부터 최대한 탐색한 뒤
그 다음 RHS 부분을 탐색하고
둘 다 존재하지 않을 때, 혹은 이미 탐색한 노드일 때
현재 노드의 값을 추가합니다.
"""
def traversePostOrder(self, node=None):
if node is None:
node = self.root
ret = []
if node.getLHS() is not None:
ret = ret + self.traversePreOrder(node.getLHS())
if node.getRHS() is not None:
ret = ret + self.traversePreOrder(node.getRHS())
ret.append(node.getValue())
return ret
다음은 너비 우선 탐색법에 대해 알아보겠습니다. 이 방법은 같은 높이에 있는 것부터 탐색합니다. 루트 노드부터 탐색을 하게 되며 위쪽 레벨(level)의 노드를 모두 거치고 난 후 아래쪽 레벨로 내려갑니다. 아래 그림처럼 탐색이 이루어집니다.

이미지 출처 : towardsdatascience.com
너비 우선 탐색법은 큐(Queue)를 사용하여 값을 뽑아냅니다. 가장 먼저 루트 노드의 값을 Enqueue 해줍니다. 다음 단계부터는 만들어진 큐에서 하나씩을 Dequeue 하게 되며 동시에 Dequeue 하는 값이 있는 노드의 자식 노드의 값을 Enqueue 해줍니다. Dequeue한 값이 있는 노드가 리프 노드라면 아무것도 Enqueue 해주지 않습니다. 위 그림에서는 다음과 같이 큐의 요소가 변하며 너비 우선 탐색이 이루어지는 것을 알 수 있습니다.
Current
Queue
1
1
2, 3
2
3, 4, 5
3
4, 5, 6, 7
4
5, 6, 7, 8
5
6, 7, 8
6
7, 8, 9, 10
7
8, 9, 10
8
9, 10
9
10
10
아래는 Breadth First Traverse를 파이썬 코드로 구현한 것입니다.
def traverseLevelOrder(self):
"""
먼저 큐를 만들고 루트 노드의 값을 추가해줍니다.
"""
ret = []
Q = Queue()
Q.enqueue(self.root)
"""
아래의 과정을 큐가 비어있을 때까지 반복합니다.
"""
while not Q.isEmpty():
"""
첫 번째 값을 Dequeue하여 뽑아냅니다.
"""
node = Q.dequeue()
if node is None:
continue
ret.append(node.getValue())
"""
그 노드의 자식 노드,
즉 LHS와 RHS가 가리키는 값을 Enqueue합니다.
"""
if node.getLHS() is not None:
Q.enequeue(node.getLHS())
if node.getRHS() is not None:
Q.enequeue(node.getRHS())
return ret
트리 구조의 성능
다음은 연결된 리스트와 일반적인 이진 탐색 트리, 그리고 최악의 경우인 이진 탐색 트리에서의 탐색, 삽입, 삭제, Traversing Operation의 성능을 비교한 표입니다. 아래에서 최악의 경우인 이진 탐색 트리는 어떻게 생겼을까요? 이곳 에서 다루었던 Degenerate Tree의 경우가 최악의 경우에 속합니다. 리프 노드 이전 노드까지의 모든 노드가 자식 노드를 하나만 갖는다면 레퍼런스가 갈라지는 부분이 없기 때문에 연결된 리스트와 탐색 시간이 같아지게 됩니다. 하지만 대부분의 경우 이진 탐색 트리에서 특정 요소를 찾는 Operation의 시간 복잡도는 $O(\log n)$ 으로 연결된 리스트의 $O(n)$ 보다 이상적입니다.
Linked List
Binary Search Tree in Average
Binary Search Tree in Worst Case
Search
$O(n)$
$O(\log n)$
$O(n)$
Insert after search
$O(1)$
$O(1)$
$O(1)$
Delete after search
$O(1)$
$O(1)$
$O(1)$
Traversing
$O(n)$
$O(n)$
$O(n)$
본 게시물은 문일철 교수님의 데이터 구조 및 분석을 참조하여 작성하였습니다.
이진 탐색 트리 (Binary Search Tree)
이진 탐색 트리(Binary Search Tree, BST) 는 차수(Degree)가 2인 트리입니다. 연결된 리스트(Linked List)가 해결해주지 못하는 탐색(Search)을 최적화하기 위해 고안된 자료구조입니다. 이런 특성 때문에 이름에도 탐색(Search)이 붙었습니다. 이진 탐색 트리가 데이터를 빠르게 탐색할 수 있는 비결은 무엇일까요? 해답은 이진 탐색 트리가 데이터를 보관하는 방법에 대한 특별한 규칙(Rule)에 있습니다. 아래는 한 이진 탐색 트리의 예시입니다.

이미지 출처 : 위키피디아 - 이진 탐색 트리
위 트리에는 어떤 규칙이 있는 것일까요? 루트와 그 자식 노드에 해당하는 두 노드를 봅시다. 루트의 값은 8이며 왼쪽 자식 노드의 값은 3, 오른쪽 자식 노드의 값은 10입니다. 루트를 기준으로 더 작은 값은 왼쪽 자식 노드로, 더 큰 값은 오른쪽 자식 노드로 배치된 것을 볼 수 있습니다. 다음에는 아래로 내려가 값이 3인 노드와 그 자식 노드를 봅시다. 이 세 노드도 마찬가지로 3보다 작은 값인 1은 왼쪽 자식 노드로, 6은 오른쪽 자식 노드로 배치된 것을 볼 수 있습니다.
이진 탐색 트리의 모든 값은 이 규칙을 따라 배치됩니다. 부모 노드보다 값이 큰 노드는 오른쪽에, 값이 작은 노드는 왼쪽에 배치됩니다. 이런 규칙이 있기 때문에 더욱 빠르게 찾을 수 있습니다. 연결된 리스트에서의 탐색 과정과 비교해 보겠습니다. $8, 3, 10, 1, 6, 14, 4, 7, 13$ 이 차례대로 저장된 연결된 리스트와 이진 탐색 트리가 있다고 해봅시다. 연결된 리스트에서 $13$ 을 찾기 위해서는 모든 요소와 비교를 해야 하므로 총 9번의 Operation을 거쳐야 합니다. 하지만 이진 탐색 트리에서는 $8, 10, 14, 13$ 만 비교하면 되니 4번의 Operation 만으로 원하는 탐색을 할 수 있습니다. 이진 탐색 트리의 탐색에 대해서는 아래에서 더 자세히 살펴보겠습니다.
Structure
연결된 리스트의 노드 하나에는 총 2개의 레퍼런스가 있었습니다. 하나는 값을 가리키는 레퍼런스이고 나머지 하나는 다음 노드를 가리키는 레퍼런스로, 넥스트(Next)라고 불렀습니다. 이진 탐색 트리는 가리켜야 하는 노드가 2개이기 때문에 총 3개의 레퍼런스를 가지고 있습니다. 그 중 왼쪽 자식 노드를 가리키는 레퍼런스를 LHS(Left Hand Side)라고 하고, 오른쪽 자식 노드를 가리키는 레퍼런스는 RHS(Right Hand Side)라고 합니다.
연결된 리스트가 헤드를 통해서만 다른 노드에 접근할 수 있었던 것처럼 트리 역시 첫 번째에 해당하는 루트를 통해서만 다른 노드에 접근할 수 있습니다. 아래는 이진 탐색 트리의 노드를 파이썬 코드로 구현한 것입니다.
class TreeNode:
nodeLHS = None
nodeRHS = None
nodeParent = None
value = None
def __init__(self, value, nodeParent):
self.value = value
self.nodeParent = nodeParent
"""각 레퍼런스 설정하기"""
def getLHS(self):
return self.nodeLHS
def getRHS(self):
return self.nodeRHS
def getParent(self):
return self.nodeParent
def getValue(self):
return self.value
def setLHS(self):
self.nodeLHS = nodeLHS
def setRHS(self):
self.nodeRHS = nodeRHS
def setParent(self):
self.nodeParent = Parent
def setValue(self):
self.value = value
아래는 이진 탐색 트리의 루트와 이진 탐색 트리에서 가능한 여러 Operation을 파이썬 코드로 적어놓은 것입니다.
from bst import TreeNode
class BinarySearchTree:
root = None
def __init__(self):
pass
def insert(self, value, node=None):
"..."
def search(self, value, node=None):
"..."
def delete(self, value, node=None):
"..."
def findMax(self, node=None):
"..."
def findMin(self, node=None):
"..."
def traverseLevelOrder(self):
"..."
def traverseInOrder(self, node=None):
"..."
def traversePreOrder(self, node=None):
"..."
def traversePostOrder(self, node=None):
"..."
이진 탐색 트리에서의 탐색
이진 탐색 트리 속에 우리가 원하는 값이 있는지 없는지 탐색(Search)하는 과정을 알아봅시다. 이진 탐색 트리에서 데이터를 저장할 때 세웠던 규칙이 빛을 발할 때가 되었습니다. 탐색하려는 값이 우리가 보고 있는 노드의 값보다 클 경우에는 RHS를 따라 이동하고, 작을 경우에는 LHS를 따라 이동합니다. 이전처럼 우리가 원하는 값을 발견할 경우에는 True를 반환하고 그렇지 않은 경우에는 다시 같은 과정을 재귀적으로(Recursive) 수행합니다. 재귀적으로 아래쪽으로 내려가다가 자식 노드가 없을 경우, 즉 리프 노드의 값이 우리가 원하는 값이 아닐 경우에는 False를 반환하고 함수를 끝마칩니다.
위에서 사용한 예시를 다시 가져와 보겠습니다.

이미지 출처 : 위키피디아 - 이진 탐색 트리
위와 같은 이진 탐색 트리에서 $13$ 을 찾기 위해서는 어떻게 해야할까요? 가장 먼저 할 수 있는 것은 루트 노드로 접근하여 값을 비교하는 것입니다. $13$ 은 $8$ 보다 크므로 RHS를 따라 이동합니다. 다음 노드의 값은 $10$ 입니다. $13$ 은 $10$ 보다도 크기 때문에 또 RHS를 따라 이동합니다. 다음 노드의 값은 $14$ 입니다. $13$ 은 $14$ 보다 작기 때문에 LHS를 따라 이동합니다. 그 다음 노드의 값이 우리가 찾던 $13$ 이므로 True를 반환하고 함수를 마칩니다.
트리에 없는 값을 탐색하는 과정도 보겠습니다. $5$ 는 어떻게 탐색할 수 있을까요? 나머지 규칙은 위와 같습니다. 루트로 접근하여 $5$ 가 $8$ 보다 작으므로 LHS를 따라 이동, $3$ 보다는 크므로 RHS를 따라 이동, $6$ 보다는 작으므로 LHS를 따라 이동합니다. 다음 노드의 값은 $4$ 입니다. $5$ 가 $4$ 보다 크기 때문에 RHS를 따라 이동해야 하는데 더 이상 이동할 노드가 없습니다. 그러므로 False를 반환하고 함수를 마치게 됩니다.
아래의 코드는 이진 탐색 트리에서의 탐색을 파이썬 코드로 구현한 것입니다.
def search(self, value, node=None):
"""
같은 값을 발견하면 True를 반환하도록 합니다.
"""
if node is None:
node = self.root
if value == node.getValue():
return True
"""
그렇지 않은 경우 크기비교를 하며 RHS, LHS로 나아가게 되고
일치하는 값을 찾지 못하고 빈 노드를 만나면 False를 반환합니다.
"""
if value > node.getValue():
if node.getRHS() is None:
return False
else:
return self.search(value, node.getRHS())
if value < node.getValue():
if node.getLHS() is None:
return False
else:
return self.search(value, node.getLHS())
이진 탐색 트리에서의 삽입
이진 탐색 트리에서의 삽입(Insert)하는 과정에 대해 알아봅시다. 삽입은 탐색과 매우 유사합니다. 삽입을 규칙에 맞게 하기 때문에 탐색이 쉬운 것이니까요.
삽입 역시 삽입 하려는 값이 해당 노드보다 작으면 LHS를 따라 이동하고, 크면 RHS를 따라 이동하는 과정을 재귀적으로 반복합니다. 탐색에서 원하는 값이 발견되면 True를 반환하였지만, 삽입은 원하는 값이 있으면 아무것도 반환하지 않고 그대로 함수를 마칩니다. 그리고 탐색에서는 더 이상 내려갈 자식 노드가 없으면 False를 반환했지만, 삽입에서는 그 자리에 우리가 원하는 값이 담긴 노드를 배치하고 함수를 마치게 됩니다. 삽입도 같은 예시를 통해 알아봅시다.

이미지 출처 : 위키피디아 - 이진 탐색 트리
탐색 과정에서 트리에 없었던 $5$ 를 삽입해 보겠습니다. 탐색과 같은 과정을 거쳐 $8, 3, 6, 4$ 를 따라 이동합니다. 탐색은 $4$ 이하에 RHS를 따라 이동할 노드가 없었기 때문에 False를 반환했지만 삽입은 그 자리에 $5$ 를 삽입하고 함수를 마치게 됩니다.
아래의 코드는 이진 탐색 트리에서의 삽입을 파이썬 코드로 구현한 것입니다.
def insert(self, value, node=None):
"""
재귀 탈출 조건문 설정하기
노드가 채워져 있지 않을 경우에는 값을 할당하도록 되어있습니다.
"""
if node is None:
node = self.root
if self.root is None:
self.root = TreeNode(value, None)
return
"""
값이 같을 경우 그대로 반환
값이 큰 경우 RHS를 따라 이동하여 재귀를 통해 같은 함수를 실행
값이 작은 경우 LHS를 따라 이동하여 재귀를 통해 같은 함수를 실행
둘 모두 값이 존재하지 않을 경우에는 해당 값을 할당하도록 합니다.
"""
if value == node.getValue():
return
if value > node.getValue():
if node.getRHS() is None:
node.setRHS(TreeNode(value, node))
else:
self.insert(value, node.getRHS())
if value < node.getValue():
if node.getLHS() is None:
node.setLHS(TreeNode(value, node))
else:
self.insert(value, node.getLHS())
return
이진 탐색 트리에서의 삭제
다음은 삭제를 알아볼 차례입니다. 이진 탐색 트리에서의 삭제는 이전의 자료 구조보다 훨씬 더 까다롭습니다. 이진 탐색 트리에서 노드를 삭제하는 경우의 수는 3개이므로 각각을 나누어 생각해야 합니다.
첫 번째는 자식 노드를 갖지 않는, 즉 리프 노드의 값을 삭제하는 경우입니다. 가장 간단한 케이스이기도 합니다. 이 때는 해당 노드의 부모 노드가 가리키는 레퍼런스를 제거함으로써 값을 삭제할 수 있습니다. 아래 그림을 봅시다.

이미지 출처 : javatpoint.com
위 그림은 85를 삭제하는 과정을 이미지로 나타낸 것입니다. 이 노드를 가리키고 있는 부모 노드의 레퍼런스를 제거하면 아무 노드의 가리킴도 받지 않는 85가 있는 노드는 가비지 컬렉터(Garbage collector)에 의해서 삭제됩니다.
두 번째는 하나의 자식 노드를 갖는 노드의 값을 삭제하는 경우입니다. 이 케이스는 연결된 리스트에서 요소를 삭제하는 경우와도 유사합니다. 방법은 삭제하려는 값이 담긴 노드를 가리키는 레퍼런스를 그 자식 노드를 가리키도록 하게 됩니다. 아래 그림을 보겠습니다.

이미지 출처 : javatpoint.com
위 그림은 12를 삭제하는 과정을 이미지로 나타낸 것입니다. 이 노드를 가리키고 있는 레퍼런스를 12가 있는 자식 노드인 6을 가리키도록 합니다. 이전 케이스와 같이 아무 레퍼런스의 가리킴도 받지 못하게 된 12는 가비지 컬렉터에 의해서 사라지게 됩니다.
마지막은 삭제하려는 값이 있는 노드가 두 개의 자식 노드를 갖는 경우입니다. 가장 까다로운 경우입니다. 기본적인 아이디어는 기존에 트리에 존재하는 다른 값으로 대체하여 넣어준 뒤에 중복되는 값을 삭제하는 것입니다. 아래 그림을 보겠습니다.

이미지 출처 : 데이터 구조 및 분석 수업자료
이번 케이스는 2가지 경우의 수가 있습니다. 위 그림은 맨 아래에 있는 이진 탐색 트리에서 $3$ 을 제거할 때의 2가지 경우의 수를 나타낸 것입니다.
왼쪽 경로는 $3$ 대신 $4$ 를 복사해 넣은 후 $4$ 에 해당하는 리프 노드를 삭제하는 과정으로 이루어져 있습니다. 리프 노드는 첫 번째로 알아보았던 그리고 오른쪽 경로는 $3$ 대신 $2$ 를 복사해 넣은 후 원래 $2$ 가 있던 노드를 삭제하는 과정으로 이루어져 있지요. 이렇게 새롭게 생성된 이진 탐색 트리는 기존의 규칙을 깨뜨리지 않습니다. 왼쪽 경로에서 $4$ , 오른쪽 경로에서 $2$ 라는 값은 어떻게 선택되는 것일까요?
일단 아무 값이나 선택하는 것은 안됩니다. 예를 들어, $3$ 이 있던 자리에 $0$ 을 넣고 원래 $0$ 이 있는 노드를 삭제하게 되면 트리의 규칙이 깨져버리기 때문입니다. 선택하는 논리는 비교적 간단합니다. $3$ 보다 왼쪽에 있는 하위 트리(Sub tree)에서는 가장 큰 값을, 오른쪽에 있는 하위 트리에서는 가장 작은 값을 선택하면 됩니다.
왼쪽에 있는 하위 트리에서 가장 큰 값이라도 오른쪽 하위 트리의 모든 값보다는 작으므로 이 값을 삭제하려는 노드에 중복시켜 넣어준 후 원래 노드를 삭제시키면 트리의 규칙을 어기지 않습니다. 오른쪽에 있는 하위 트리에서 가장 작은 값 역시 왼쪽 하위 트리에 있는 모든 값보다는 크기 때문에 삭제하려는 노드에 중복해준 후 원래 값이 있는 노드를 삭제시켜도 트리의 규칙을 어기지 않음을 알 수 있습니다.
트리에서 이런 값을 찾는 방법 역시 간단합니다. 먼저 왼쪽 하위 트리의 최댓값을 찾는 경우 (그림에서 오른쪽 경로) 부터 생각해봅시다. 이 경우는 삭제하려는 값이 있는 노드의 LHS를 따라 한 번 내려간 뒤, 이후부터는 항상 RHS만을 따라갑니다. 만약 더 이상 RHS가 없는 노드가 있다면 그 노드의 값이 중복해줄 값으로 선택됩니다. 위의 예시에서도 $3$ 이 있는 노드의 LHS를 따라 한 번 내려가면 $2$ 가 있는 노드가 됩니다. 다음부터는 RHS 만을 따라 내려가야 하지만 해당 노드에서 RHS가 없으므로 해당 노드의 값인 $2$ 가 삭제할 값을 대체하는 값이 됩니다. 다음으로 오른쪽 하위 트리의 최솟값을 찾는 경우 (그림에서 왼쪽 경로) 를 생각해봅시다. 위 그림에서 왼쪽 방향에 있는 3을 4로 대체한 것은 첫 번째 방법을 따른 것이고, 오른쪽 방향에 있는 3을 2로 대체한 것은 두 번째 방향을 따른 것이다. 이 때는 반대로 삭제하려는 값이 있는 노드의 RHS를 따라 한 번 내려간 뒤, 이후부터는 항상 LHS만을 따라갑니다. 그리고 더 이상 LHS가 없는 노드가 있다면 그 노드의 값이 중복해줄 값으로 선택됩니다. 위의 예시에서도 $3$ 이 있는 노드의 RHS를 따라 한 번 내려가면 $5$ 가 있는 노드가 됩니다. 다음부터는 LHS 만을 따라 내려가야 하므로 한 번 더 이동한 노드의 값은 $4$ 입니다. 다음에 또 LHS를 따라 이동해야 하지만 해당 노드에서 LHS가 없으므로 해당 노드의 값인 $4$ 가 삭제할 값을 대체하는 값이 됩니다.
이렇게 복제된 값을 담고 있는 노드는 LHS나 RHS 중 하나의 레퍼런스가 없는 노드이므로 위에서 나왔던 리프 노드를 삭제하는 방법이나, 자식 노드가 하나인 노드를 삭제하는 방법을 사용하여 처리가 가능합니다. 아래는 모든 삭제 과정을 파이썬 코드로 구현한 것입니다.
def delete(self, value, node=None):
if node is None:
node = self.root
"""
삭제하려는 값을 찾아가는 과정
"""
if node.getValue() < value:
return self.delete(value, node.getRHS())
if node.getValue() > value:
return self.delete(value, node.getLHS())
"""
삭제하려는 값이 있는 노드를 만났을 때
"""
if node.getValue() == value:
"""
2개의 자식을 갖는 노드의 값 삭제하기
여기서는 2가지 방법 중
RHS로 이동 후 RHS에서 가장 왼쪽 값(최솟값)을
찾아 대체하는 방법을 사용하였습니다.
"""
if node.getLHS() is not None and node.getRHS() is not None:
nodeMin = self.findMin(node.getRHS())
node.setValue(nodeMin.getValue())
self.delete(nodeMin.getValue(), nodeRHS())
return
parent = node.getParent()
"""
자식 노드를 1개 갖는 노드의 값을 삭제하는 코드입니다.
"""
if node.getLHS() is not None:
if node == self.root:
self.root = node.getLHS()
elif parent.getLHS() == node:
parent.getLHS(node.getLHS())
node.getLHS().setParent(parent)
else:
parent.setRHS(node.getLHS())
node.getLHS().setParent(parent)
return
if node.getRHS() is not None:
if node == self.root:
self.root = node.getRHS()
elif parent.getLHS() == node:
parent.getLHS(node.getRHS())
node.getRHS().setParent(parent)
else:
parent.setRHS(node.getRHS())
node.getRHS().setParent(parent)
return
"""
자식을 갖지 않는 노드의 값을 삭제하는 경우입니다.
"""
if node == self.root:
self.root = None
elif parent.getLHS() == node:
parent.setLHS(None)
else:
parent.setRHS(None)
return
위 코드에 있는 findMax 와 findMin 함수 역시 따로 정의를 해주어야 합니다. 아래와 같이 각 함수를 정의할 수 있습니다.
def findMax(self, node=None):
if node is None:
node = self.root
if node.getRHS() is None:
return node
return self.findMax(node.getRHS())
def findMin(self, node=None):
if node is None:
node = self.root
if node.getLHS() is None:
return node
return self.findMin(node.getLHS())
Traversing
Traverse는 ‘가로지르다’라는 뜻을 가진 단어입니다. 연결된 리스트나 배열에서 존재하지 않았던 Traversing 이란 말 그대로 모든 노드를 가로지르며 값을 훑는 것입니다. 이전에 배웠던 자료구조는 중간에 갈라지는 길이 없으므로 탐색(Search)하면서 모든 노드를 다 거칠 수 있었습니다. 하지만 트리에서는 길이 나누어지므로 값을 찾는 탐색만으로 모든 노드를 거쳐갈 수 없게 되지요.
Traversing의 방법은 크게 깊이 우선 탐색법(Depth first search, DFS) 과 너비 우선 탐색법(Breadth first search, BFS) 두 가지로 나뉩니다. 먼저 깊이 우선 탐색법에 대해 알아봅시다. 깊이 우선 탐색법은 순서에 따라 3가지 방법이 있습니다. 첫 번째가 현재 노드의 값을 탐색한 후 LHS, RHS 순서로 탐색하는 Pre-order Traverse 입니다. 두 번째는 LHS를 먼저 탐색하고 현재 노드의 값을 탐색한 후 RHS값을 탐색하는 In-order Traverse 입니다. 마지막 방법으로는 LHS와 RHS를 모두 탐색한 후 맨 마지막에 현재 노드의 값을 탐색하는 Post-order Traverse가 있습니다. 아래의 트리를 보며 설명을 이어나가겠습니다. 아래의 노드를 각 방법으로 Traversing 해보겠습니다.

이미지 출처 : towardsdatascience.com
먼저 Pre-order 방식입니다. 앞서 말했던 것처럼 이 방식은 현재 노드 - LHS를 따라 내려간 노드 - RHS를 따라 내려간 노드 순으로 탐색합니다. 아래 그림과 같은 방법으로 탐색이 이루어집니다. 접근하는 노드의 값을 무조건 얻기 때문에 루트 노드 부터 탐색하는 것을 볼 수 있습니다.

이미지 출처 : towardsdatascience.com
다음은 In-order 방식입니다. 이 방식은 LHS를 따라 내려간 노드 - 현재 노드 - RHS를 따라 내려간 노드 순으로 탐색합니다. 아래 그림과 같은 방법으로 탐색이 이루어집니다. 현재 노드의 값을 얻지 않고 일단 LHS가 없을 때까지 내려가기 때문에 가장 왼쪽 아래에서부터 탐색이 시작되는 것을 볼 수 있습니다.

이미지 출처 : towardsdatascience.com
다음은 Post-order 방식입니다. 이 방식은 LHS를 따라 내려간 노드 - RHS를 따라 내려간 노드 - 현재 노드 순으로 탐색합니다. 아래 그림과 같은 방법으로 탐색이 이루어집니다. 현재 노드의 값을 얻지 않고 일단 LHS와 RHS가 모두 없을 때까지 내려가기 때문에 가장 왼쪽 아래에서부터 아래쪽을 다 훑고 난 후에 위로 올라오는 방향으로 탐색이 되는 것을 볼 수 있습니다.

이미지 출처 : towardsdatascience.com
각각의 깊이 우선 탐색 과정을 파이썬 코드로 구현하면 다음과 같습니다.
"""
일단 현재 노드의 값을 추가한 뒤
LHS, RHS 순으로 탐색합니다.
"""
def traversePreOrder(self, node=None):
if node is None:
node = self.root
ret = []
ret.append(node.getValue())
if node.getLHS() is not None:
ret = ret + self.traversePreOrder(node.getLHS())
if node.getRHS() is not None:
ret = ret + self.traversePreOrder(node.getRHS())
return ret
"""
일단 현재 LHS 부분부터 최대한 탐색한 뒤
현재 노드의 값을 추가하고 그 다음 RHS 부분을 탐색합니다.
"""
def traverseInOrder(self, node=None):
if node is None:
node = self.root
ret = []
if node.getLHS() is not None:
ret = ret + self.traversePreOrder(node.getLHS())
ret.append(node.getValue())
if node.getRHS() is not None:
ret = ret + self.traversePreOrder(node.getRHS())
return ret
"""
일단 현재 LHS 부분부터 최대한 탐색한 뒤
그 다음 RHS 부분을 탐색하고
둘 다 존재하지 않을 때, 혹은 이미 탐색한 노드일 때
현재 노드의 값을 추가합니다.
"""
def traversePostOrder(self, node=None):
if node is None:
node = self.root
ret = []
if node.getLHS() is not None:
ret = ret + self.traversePreOrder(node.getLHS())
if node.getRHS() is not None:
ret = ret + self.traversePreOrder(node.getRHS())
ret.append(node.getValue())
return ret
다음은 너비 우선 탐색법에 대해 알아보겠습니다. 이 방법은 같은 높이에 있는 것부터 탐색합니다. 루트 노드부터 탐색을 하게 되며 위쪽 레벨(level)의 노드를 모두 거치고 난 후 아래쪽 레벨로 내려갑니다. 아래 그림처럼 탐색이 이루어집니다.

이미지 출처 : towardsdatascience.com
너비 우선 탐색법은 큐(Queue)를 사용하여 값을 뽑아냅니다. 가장 먼저 루트 노드의 값을 Enqueue 해줍니다. 다음 단계부터는 만들어진 큐에서 하나씩을 Dequeue 하게 되며 동시에 Dequeue 하는 값이 있는 노드의 자식 노드의 값을 Enqueue 해줍니다. Dequeue한 값이 있는 노드가 리프 노드라면 아무것도 Enqueue 해주지 않습니다. 위 그림에서는 다음과 같이 큐의 요소가 변하며 너비 우선 탐색이 이루어지는 것을 알 수 있습니다.
| Current | Queue |
|---|---|
| 1 | |
| 1 | 2, 3 |
| 2 | 3, 4, 5 |
| 3 | 4, 5, 6, 7 |
| 4 | 5, 6, 7, 8 |
| 5 | 6, 7, 8 |
| 6 | 7, 8, 9, 10 |
| 7 | 8, 9, 10 |
| 8 | 9, 10 |
| 9 | 10 |
| 10 |
아래는 Breadth First Traverse를 파이썬 코드로 구현한 것입니다.
def traverseLevelOrder(self):
"""
먼저 큐를 만들고 루트 노드의 값을 추가해줍니다.
"""
ret = []
Q = Queue()
Q.enqueue(self.root)
"""
아래의 과정을 큐가 비어있을 때까지 반복합니다.
"""
while not Q.isEmpty():
"""
첫 번째 값을 Dequeue하여 뽑아냅니다.
"""
node = Q.dequeue()
if node is None:
continue
ret.append(node.getValue())
"""
그 노드의 자식 노드,
즉 LHS와 RHS가 가리키는 값을 Enqueue합니다.
"""
if node.getLHS() is not None:
Q.enequeue(node.getLHS())
if node.getRHS() is not None:
Q.enequeue(node.getRHS())
return ret
트리 구조의 성능
다음은 연결된 리스트와 일반적인 이진 탐색 트리, 그리고 최악의 경우인 이진 탐색 트리에서의 탐색, 삽입, 삭제, Traversing Operation의 성능을 비교한 표입니다. 아래에서 최악의 경우인 이진 탐색 트리는 어떻게 생겼을까요? 이곳 에서 다루었던 Degenerate Tree의 경우가 최악의 경우에 속합니다. 리프 노드 이전 노드까지의 모든 노드가 자식 노드를 하나만 갖는다면 레퍼런스가 갈라지는 부분이 없기 때문에 연결된 리스트와 탐색 시간이 같아지게 됩니다. 하지만 대부분의 경우 이진 탐색 트리에서 특정 요소를 찾는 Operation의 시간 복잡도는 $O(\log n)$ 으로 연결된 리스트의 $O(n)$ 보다 이상적입니다.
| Linked List | Binary Search Tree in Average | Binary Search Tree in Worst Case | |
|---|---|---|---|
| Search | $O(n)$ | $O(\log n)$ | $O(n)$ |
| Insert after search | $O(1)$ | $O(1)$ | $O(1)$ |
| Delete after search | $O(1)$ | $O(1)$ | $O(1)$ |
| Traversing | $O(n)$ | $O(n)$ | $O(n)$ |

Comments